CS 180 Portfolio

Original Image

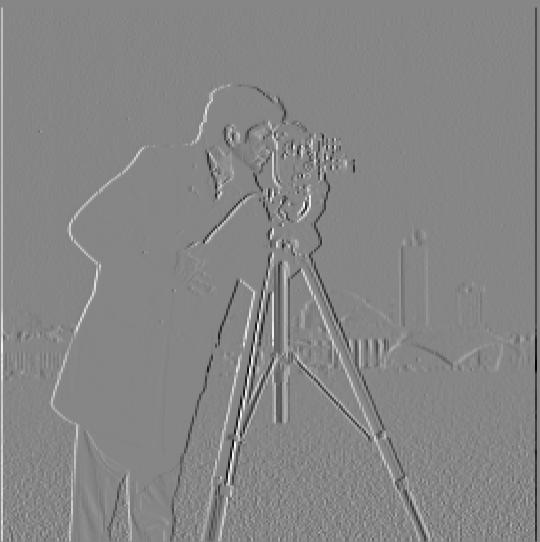
We applied various filters to explore different image processing techniques. Below are examples of different filters applied to the same original image. The first row is using finite difference operators, and the second row is using the finite difference operators after applying a Gaussian Blur. The resulting edge image detection was better after thee Gaussian blur and also having a lower threshold.

d_x camerman

d_y camerman

Gradient Magnitude

Edge Image, 0.20 Threshold

DoGDx

DoGDy

Gaussian Gradient Magnitude

Gaussian Edge Image, 0.09 Threshold

We could also convolve the filters with the Gaussian, and then apply the resulting filter on the camera, and we would get the same result.

d_x of gaussian

d_y of gaussian

Gradient Magnitude

Gaussian Gradient Magnitude

We will sharpen our images by taking our image, subtract the low frequencies to create an image with higher frequencies, then enhance the original image with the said higher frequencies.

Original Image

Sharpened Image

Blurred Image

Resharpened Image

The first image is the original image. The second image is the result of adding the higher frequencies. The third image is the result of blurring the original image. The final image is the result of sharpening the blurred image. The resulting "resharpened" image is not much worse than the original image.

Original Image

Sharpened Image

Blurred Image

Resharpened Image

For my choice of image, I chose to do a skyline of SF. My findings are consistent with the results from running the filters on the Taj picture.

Original Image

Unsharp Masking Result

Hybrid images combine low-frequency components of one image with high-frequency components of another. This creates an image that appears different when viewed from near and far distances. We experimented with various cutoff frequencies and image pairs.

Image 1 (Derek)

Image 2 (Nutmeg)

Hybrid Image (Derek + Nutmeg)

For my first hybrid image, I chose two of my favorite sports athletes: NBA Legend Lebron James and MLB superstar Shohei Ohtani. Thus, I"ve created a new sports superstar: LeBron Ohtani.

Image 1 (LeBron James)

Image 2 (Shohei Ohtani)

Hybrid Image (Lebron Ohtani)

As for my second hybrid image, I created New Francisco, a mix of San Francisco and New York City. This didn"t work out too well because they were too similar, interestingly enough. It was hard to differentiate the two, especially in black and white image, up close. This is interesting because the earlier ones that failed for me were hybrid images that were too different.

Image 1 (SF)

Image 2 (NYC)

Hybrid Image (NYC/SF)

As for my second hybrid image, I created New Francisco, a mix of San Francisco and New York City. This didn"t work out too well because they were too similar, interestingly enough. It was hard to differentiate the two, especially in black and white image, up close. This is interesting because the earlier ones that failed for me were hybrid images that were too different.

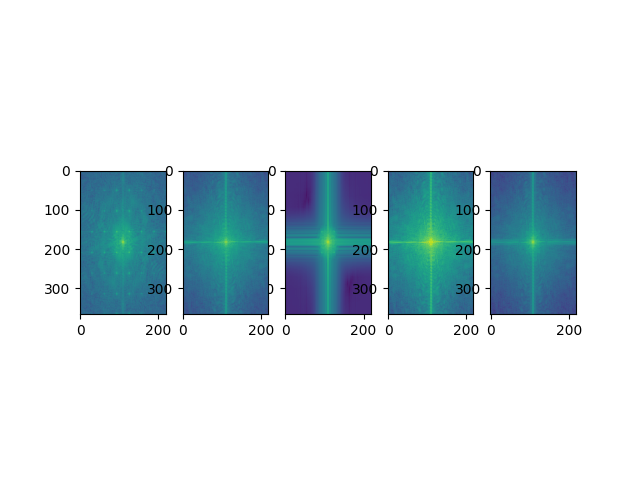
This is the resulting outputs of the log fourier transformation of the Othani/Lebron picture. The first image (left to right) is the Lebron image, the second is the Ohtani image, the third is the Low frequencies of Lebron,the fourth are the high frequencies of Ohtani, and the final is the hybrid image.

Finally, we used different filters to seamlessly blend two different pictures. The first step in this process was to create Gaussian and Laplacian stacks. A Gaussian stack is repeatedly convolving the image with a Gaussian to blur the picture, and then the Laplacian is created by subtracting each element in the Gaussian stack with the next one.

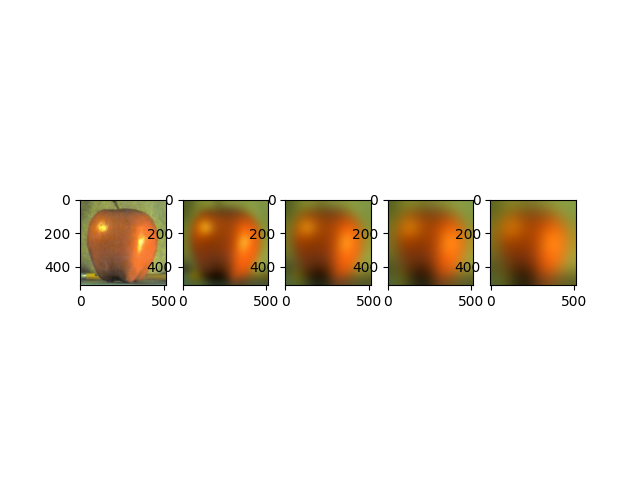
apple gaussian stack

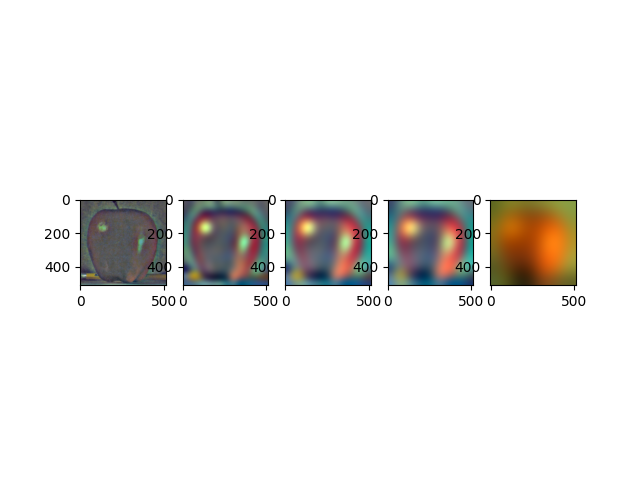
apple laplacian stack

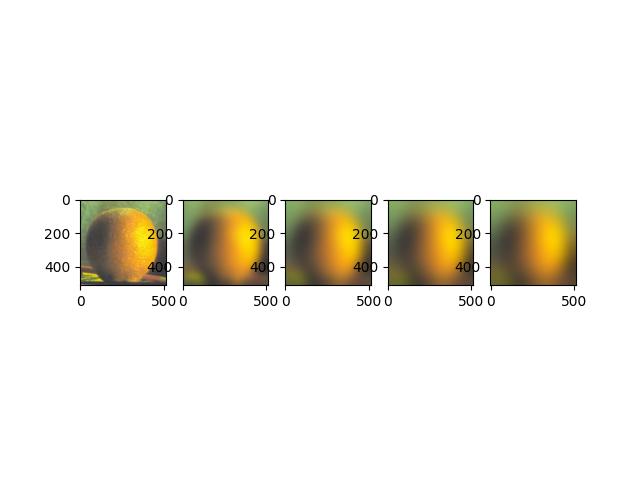
orange gaussian stack

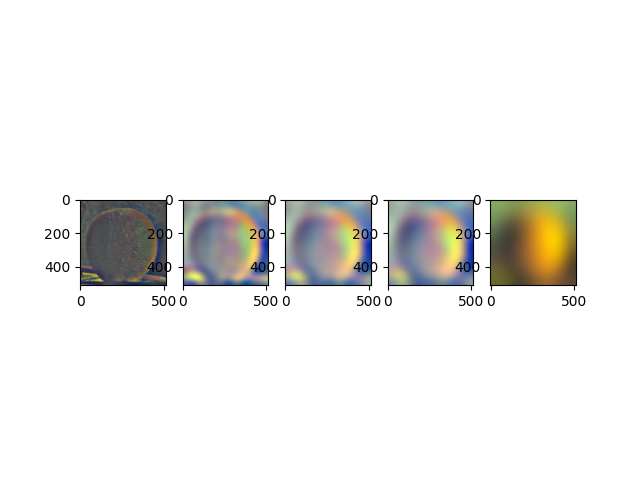
orange laplacian stack

We then used the Gaussian and Laplacian stacks with a Gaussian stack of a mask to blend the two. Below are are the results of blending two pictures.

Oraple (orange, apple)

SFYC (SF + NYC)

Mountace (Mountains in Space)

For the last picture, I created a circular mask instead of doing a simple mask with a straight line.